El Método Simplex de Dos Fases permite abordar la resolución de aquellos modelos de Programación Lineal que luego de ser llevados a su forma estándar no permite obtener una solución básica factible inicial en las variables del modelo. Para enfrentar esta situación existen distintas estrategias algorítmicas entre las que destacan el Método Simplex de Dos Fases y el Método de la M Grande, las cuales suelen ser discutidas en cursos de Investigación Operativa (Investigación de Operaciones). En el siguiente artículo nos concentraremos en el análisis de la primera alternativa a través de un enfoque teórico – práctico.
Ejemplo Método Simplex de Dos Fases
Considere el siguiente modelo de Programación Lineal usando el Método Simplex de Dos Fases.
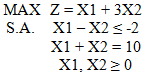
Fase I (Método Simplex de Dos Fases)
En este caso resulta conveniente multiplicar por -1 la primera restricción de modo que el lado derecho sea positivo, lo cual tiene como efecto adicional que cambia el sentido de la desigualdad. En consecuencia el problema que define la Fase I del Método Simplex de Dos Fases es:
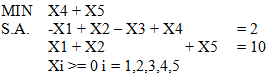
Donde X3 es variable de exceso y X4 y X5 son variables artificiales de la restricción 1 y 2 respectivamente. Luego estaos en condiciones de confeccionar la tabla inicial de la Fase I donde las variables auxiliares X4 y X5 tienen costo reducido igual a uno (dado sus respectivos coeficientes en la función objetivo de dicha fase).
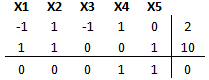
A continuación se llevan a cero los costos reducidos de X4 y X5. Para ello se realizan operaciones filas, por ejemplo, primero multiplicando por -1 la fila 1 y sumándola a la fila 3, para luego multiplicar por -1 la fila 2 y sumarla a la fila 3.
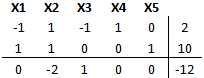
Notar ahora que las variables básicas son X4 y X5 y las variables no básicas son X1, X2 y X3. Entre las variables no básicas la que tiene costo reducido negativo es X2, por tanto dicha variable entra a la Base y mediante el criterio de factibilidad o mínimo cuociente se determina aquella variable básica que deja la base. Esto se obtiene de Min{2/1; 10/1}=2. Por tanto X4 sale de la base y se realiza una iteración.
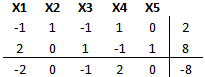
Luego de concluir la iteración se dispone ahora de dos variables no básicas con costo reducido negativo: X1 y X3. Teniendo en consideración un criterio de rapidez de convergencia se privilegia la entrada a la base de X1 al tener ésta el costo reducido más negativo. La variable básica que deja la base se obtiene de Min{8/2}=4, determinando que X5 sale de la base. Para actualizar la tabla sumamos la fila 2 a la fila 3 (de modo que el costo reducido de X1 se transforme en cero) y luego multiplicamos por 1/2 la fila 2 y la sumamos a la fila 1 (para que de esta forma X1 sea básica asociada a la fila 2, tomando la estructura de la variable básica saliente X5).
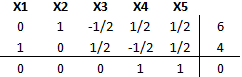
Se verifica que se concluye la Fase I del Método Simplex de Dos Fases. Esta situación se detecta cuando se dispone de una solución básica que satisface las condiciones de no negatividad, donde las variables no básicas tienen costos reducidos mayores o iguales a cero y el valor de la función objetivo es igual a cero.
Fase II (Método Simplex de Dos Fases)
A continuación se da inicio a la Fase II del Método Simplex de Dos Fases. En esta etapa se elimina las columnas asociadas a las variables auxiliares utilizadas en la Fase I del método (en el ejemplo las variables X4 y X5) y se actualiza el vector de costos reducidos considerando la función objetivo del problema original en formato de minimización, esto es MIN -X1–3X2.
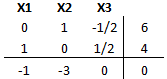
Cabe recordar que las variables básicas finalizadas la Fase I son X2 y X1 y luego de la actualización de la fila de costos reducidos (fila 3) será necesario llevar sus respectivos costos reducidos a cero, para lo cual se suma la fila 2 a la fila 3 y luego se multiplica por 3 la fila 1 y se suma a la fila 3, obteniéndose lo siguiente:
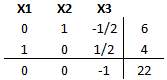
Del procedimiento anterior resulta que la variable no básica X3 tiene costo reducido y por tanto ingresa a la base. La variable básica que deja la base se obtiene de Min{4/1/2}=8 y por tanto X1 abandona la base. Con ello se realiza una iteración del método obteniendo la siguiente tabla:
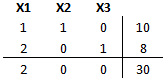
Observar que la variable no básica X1 tiene costo reducido igual a 2 (que satisface las condiciones de no negatividad), además de enfrentarnos a una solución básica factible para X2 y X3.
Por tanto se concluye la Fase II del Método Simplex de Dos Fases con solución óptima X1=0, X2=10 y X3=8 y valor óptimo V(P)=30.
